Dalam uji persyaratan analisis, penelitian
ini menggunakan uji normalitas data, uji linieritas, dan uji multikolinieritas.
a. Uji Normalitas Data
Pengujian normalitas data digunakan untuk
menguji apakah data kontinu berdistribusi normal sehingga analisis dengan
validitas, reliabilitas, uji t, korelasi, regresi
dapat dilaksanakan (Husaini, 2008: 109). Menurut Singgih yang dikutip oleh
Suparman (Galih, 2012: 54), data dalam penelitian ini
berskala interval maka dalam uji normalitas menggunakan uji Kolmogorov-Smirnov
(K-S), kriteria yang digunakan adalah apabila p > 0,05 maka sebaran data dikatakan
normal. Uji normalitas data dalam penelitian ini menggunakan program bantu SPSS
V. 16.
b. Uji Linieritas
Uji linearitas bertujuan untuk mengetahui apakah dua variabel
mempunyai hubungan yang linear atau tidak secara signifikan. Uji ini biasanya
digunakan sebagai prasyarat dalam analisis korelasi atau regresi linear. Dalam penelitian ini menggunakan bantuan program
SPSS V. 16. Pengujian pada SPSS V. 16 dengan menggunakan Test for Linearity pada taraf signifikansi 0,05. Dua variabel dikatakan
mempunyai hubungan yang linear bila signifikansi (Linearity) kurang dari 0,05.
c. Uji Multikolinieritas
Uji multikolinearitas digunakan untuk persyaratan analisis
regresi ganda, yaitu untuk mengetahui apakah hubungan antarvariabel bebas
terjadi ketergantungan atau tidak. Ketergantungan antarvariabel bebas terjadi
bila koefisien antarvariabel bebas lebih besar atau sama dengan 0,800.
Ada beberapa metode pengujian yang digunakan dalam uji multikolineritas diantaranya yaitu (1) dengan melihat nilai inflation factor (VIF) pada model
regresi, (2) dengan membandingkan nilai koefisien determinasi individual (r2) dengan nilai determinasi secara serentak (R2),
dan (3) dengan melihat nilai eigenvalue dan
condition index.
1. Uji Hipotesis
a.
Uji
Hipotesis Pertama dan Kedua
1)
Untuk
uji hipotesis pertama dan kedua langkah-langkahnya sebagai berikut:
a)
Menentukan
hipotesis
Ho
: Tidak ada pengaruh yang signifikan antara X dan Y
Ha
: Ada pengaruh yang signifikan antara X dan Y
b)
Mencari
koefisien korelasi antara predictor X dan kriterium Y dengan menggunakan rumus
korelasi product momen dari Sugiyono (2013: 228).
∑xy : Jumlah
hasil kali antara X dan Y.
∑x2 :
Jumlah kuadrat product moment dari variabel X.
∑y2 :
Jumlah kuadrat product moment dari variabel Y.
Analisis selanjutnya dengan program
bantu SPSS versi 16 dengan kriteria uji sebagai berikut :
Jika Probabilitas > 0,05 : Ho diterima
Jika Probabilitas < 0,05 : Ho ditolak
c)
Mencari nilai regresi
dengan menggunakan rumus regresi sederhana dengan satu prediktor dari Sugiyono
(2013: 261) :
Keterangan :
a,b = Koefisien regresi
Y = Variabel Terikat
X = Variabel bebas
b.
Uji
Hipotesis Ketiga
a)
Untuk
hipotesis ketiga langkah-langkahnya adalah sebagai berikut :
a)
Menentukan
hipotesis
Ho : Tidak ada pengaruh
yang signifikan antara X1,X2 dan Y
Ha
: Ada pengaruh yang signifikan antara X1,X2 dan Y
b)
Mencari
persamaan regresi ganda seperti yang dikemukakan oleh Sugiyono (2013 : 278) :
(1) ∑x1y = a1∑x12
+ a2∑x1x2
(2) ∑x2y = a1∑x1
x2 + a2∑x1x2
c)
Uji
signifikasi korelasi (F) antara kriterium Y dengan predictor X1 dan
X2 yaitu dengan menggunakan
rumus dari Sugiyono (2013: 286) :
Freg
=
Dimana
:
Freg = Harga F garis regresi
N = Banyak sampel
m = Banyaknya predictor
R2 = Koefisien korelasi antara Y terhadap X1
dan X2
Kemudian harga Freg
dikonsultasikan dengan Ftabel dengan kesimpulan sebagai berikut :
-
Apabila
Freg > Ftabel, maka Ha diterima yang berarti ada
pengaruh antara X dengan Y.
-
Apabila
Freg < Ftabel, maka Ha diterima yang berarti tidak ada
pengaruh antara X dengan Y.
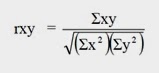


Olah Data Semarang Khusus Untuk Olah Data Frontier 4.1, DEAP 2.1
BalasHapusSPSS, AMOS, LISREL, EVIEWS, SMARTPLS, Software R
WA : +6285227746673
IG : @olahdatasemarang